La moyenne incongrue
Par Zénon Mazur
Les journaux nous abreuvent de statistiques de toutes sortes.
Règle générale, politiciens et journalistes, pour illustrer leurs analyses font appel à la moyenne. Dans plusieurs cas la moyenne est significative, mais ce n’est pas toujours le cas. La statistique la plus incongrue est la multitude de statistiques sur le revenu moyen. Prenons l’exemple d’une micro-entreprise de 5 ouvriers avec le salaire de 31 000$ chacun, d’un comptable avec un revenu de 60 000$ et le PDG avec 80 000$. En faisant le calcul de la moyenne nous nous obtenons environ 42 000$. Portant 71% des salariés gagnent moins que la moyenne. Cet exemple nous montre que la moyenne n’est pas significative, car la médiane (50% de la distribution) est 31 000$. Donc la différence entre la moyenne et la médiane est de 11 000$, ce qui représente 35% du revenu médian.
Dans les pays qu’on appelle équilibré la différence entre la moyenne et la médiane est la plus rapprochée, donc souvent il s’agit de pays moderne dotés d’un système économique bien équilibré doublé d’un filet social enviable.
Il est aussi intéressant de voir l’application de l’indice Gini et la courbe de Lorenz.
Les pays les plus égalitaires ont un coefficient de l’ordre de 0,22 (Danemark,Suède, Japon,…).
La France, Canada le coefficient de Gini est de 0,275.
La Pologne 0,38
Celui de la Chine est en train d’augmenter et avoisine désormais 0,5.
Les pays les plus inégalitaires au monde ont un coefficient de 0,6 (Brésil, Guatemala, Honduras, …).
Courbe de Lorenz et coefficient de Gini (2 fois A)
Le coefficient de Gini se calcule par rapport à la fonction (dont la représentation graphique est la courbe de Lorenz) qui associe à chaque part de la population ordonnée par revenu croissant, la part que représente ses revenus.
Aussi voir le tableau de pays OCD
******************************************************************************************
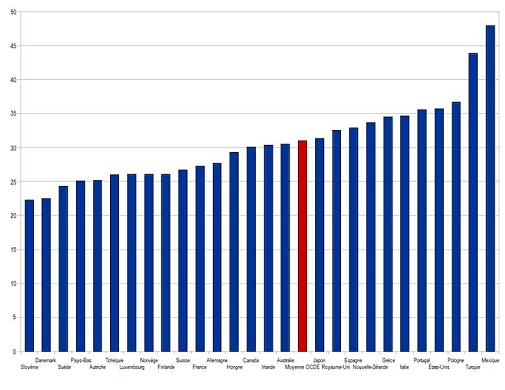